Q6. Consider a hollow frustum, closed on both ends. An ideal gas of molar mass M and temperature T is inside it. It is rotated about its short end with constant angular velocity \(\omega\). The radius on its left end is \(a\), and its right end is \(b\). Pressure on its left end is \(P_0\). The total length is \(L\). Find pressure profile. (\(P(x)\))

Idea:

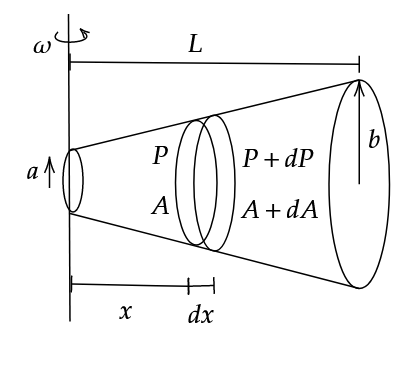
Each small part has circular motion. Hence, we can apply the following formula for an infinitesimally small section and integrate over it to find the pressure profile

\[F = m R \omega^2\tag1\]

We also have the ideal gas equation, \(PV = nRT\) with us, but we shall use its modified form

\[PM = \rho R T\tag2\]

Solution:

We shall first solve the question generally for any \(A(x)\).

Using eq. (1), we have,

\[(P+dP)(A+dA) - PA = (dm) x \omega^2\tag3\]

\[AdP + PdA = \rho A x (dx) \omega^2\]

Substituting \(\rho = \frac{PM}{RT}\) from (2),

\[AdP + PdA = \frac{PM}{RT} A \omega^2 x dx\]

\[\implies \int_{P_0}^{P} \frac{dP}{P} + \int_{A_0}^{A} \frac{dA}{A} = \frac{M\omega^2}{RT} \int_{0}^{x} x dx\]

\[\ln \left( \frac{PA}{P_0 A_0} \right) = \frac{M \omega^2 x^2}{2RT}\]

\[\therefore P = \frac{P_0 A_0}{A} e^{\frac{M \omega^2 x^2}{2RT}}\tag4\]

Where, \(A\) and \(A_0\) are functions of \(x\).

Now, according to the question, we have,

\[r = \left( \frac{b-a}{L} \right) x + a\]

\[\implies A = \pi r^2 = \pi \left( \left( \frac{b-a}{L} \right) x + a \right)^2\]

\[A_0 = \pi a^2\]

Substituting these values into (4),

\[p = \frac{P_0 a^2 L^2}{\left( (b-a) x + aL \right) ^2} e^{\frac{M \omega^2 x^2}{2RT}}\]