Q5. A frustum is made with inner radius \(a_1\) and outer radius \(a_2\) on the short end, and radii \(b_1\) and \(b_2\) on the larger side. Find the net thermal resistance offered by the hollow frustum if its total length is \(L\) and thermal conductivity is \(K\).

Solution:

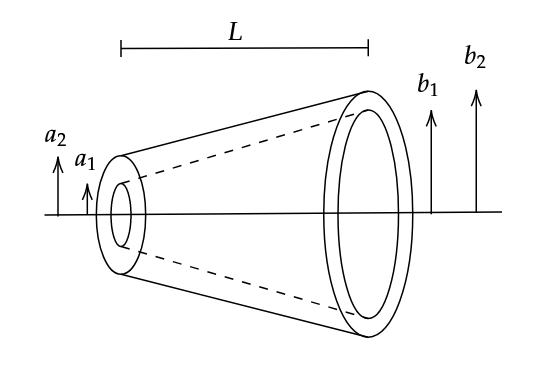
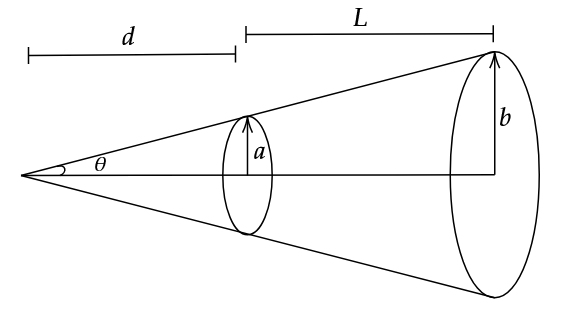
From the diagram,

\[b = a + L \tan \theta\]

\[\tan \theta = \frac{b-a}{L} = \frac{b}{L+d}\]

Cross sectional area,

\[A = \frac{\pi b (L + d)}{\cos \theta} - \frac{\pi a d}{\cos \theta}\]

\[\implies A = \frac{\pi L }{ \cos \theta} (2a + L \tan \theta)\]

Substituting this into (1),

\[dR = \frac{L}{KA} = \frac{da}{K\pi L ( 2a + L \tan \theta )}\]

\[\int dR = \frac{1}{K \pi L} \int_{a_1}^{a_2} \frac{da}{2a + L \tan \theta}\]

Substituting the value of \(\tan \theta\),

\[\therefore R = \frac{1}{2 \pi K L } \ln \left( \frac{a_2 + b_2}{a_1 + b_1} \right)\]

Here, we note that unlike regular conductors, this one is inversely proportional to the length \(L\).