Q3. Consider a 3D shape whose left end has radius \(1\)m. The shape is circular, with its radius increasing continually as \(r = a^x\), \(a \in \mathbb{R^+}\). Assume forces to be acting in the centre of the side (circular) faces on both sides. Consider it to have Young’s modulus \(Y\). Find elongation \(\Delta L\).

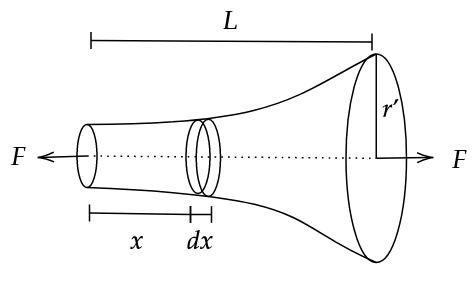
We know that,

\[\Delta L = \frac{FL}{AY}\]

Also, \[r = a^x\] can be written as \[r = e^{x \ln a}\tag1\]

Elongation in infitesimally small cross section \(dl\),

\[dl = \frac{Fdx}{\pi r^2 Y}\]

\[\Delta L = \frac{F}{\pi Y} \int_{1}^{r'} \frac{dx}{r^2}\]

Substituing (1) and corresponding change of limits,

\[\Delta L = \frac{F}{\pi Y} \int_{0}^{L} \frac{dx}{(e^{x \ln a})^2}\]

\[\Delta L = \frac{F}{\pi Y} \left( \frac{-1}{2 \ln a} e^{-2x \ln a} \right) \Biggr|_{0}^{L}\]

\[\therefore \Delta L = \frac{F}{2 \pi Y \ln a} \left( 1 - e^{-2L \ln a} \right)\]

It is interesting to note that if we let \(L \to \infty\), assuming force \(F\) on the other end can still be applied, we get that \(e^{-2L \ln a} \to 0\).

\[\implies \Delta L \Bigr|_{L = \infty} = \frac{F}{2 \pi Y \ln a}\]

So, for an infinitely large object, we can have finite elongation due to tensile forces. (Theoretically).

This is due to the fact that \(e^x\) rises rather rapidly. So, after some distance, we get that the cross sectional area \(A\) is much larger than the small \(dx\) at that point. And, as we know, \(\Delta L \propto \frac{dx}{A}\). Hence we get this finite elongation.