Q2. A table with a smooth horizontal surface is rotating with constant angular velocity \(\omega\) about the vertical axis. A groove is made radially, and a particle is placed at a distance \(a\) from the centre. Find the trajectory of the particle as a function of the angular displacement \(\theta\).

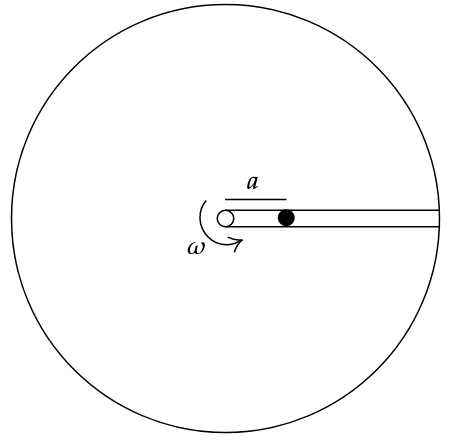
Solution:

Assuming, table to be infinitely large(ball doesn’t fall off).

Net force radially outward = \(mR\omega^2\)

Let \(r\) be the radial position at any time.

\[\ddot{x} = \omega^2 r\]

\[v \frac{dv}{dr} = \omega^2 r\]

\[\int_{0}^{v} v dv = \int_{a}^{r} \omega^2 r dr\]

\[v = \omega \sqrt{r^2 - a^2} \]

\[\int_{a}^{r} \frac{dr}{\sqrt{r^2 - a^2}} = \int_{0}^{t} \omega dt\]

\[\ln | r+\sqrt{r^2 - a^2} | \Big|_{a}^{r} = \omega t \Bigr|_{0}^{t}\]

\[\ln \frac{r+\sqrt{r^2 - a^2}}{a} = \omega t\]

\[r + \sqrt{r^2 - a^2} = a e^{\omega t}\tag1\]

Reciprocating,

\[\frac{1}{r + \sqrt{r^2 - a^2}} = \frac{e^{-\omega t}}{a}\]

Rationalising,

\[\frac{r - \sqrt{r^2-a^2}}{a^2} = \frac{e^{-\omega t}}{a}\tag2\]

Adding (1) and (2), we get

\[2r = a(e^{\omega t} + e^{-\omega t})\]

We know that, for \(\alpha = 0\), \(\omega t = \theta\).

\[\therefore r = \frac{a}{2} ( e^\theta + e^{-\theta}) = a \cosh (\theta)\]